For those who are fond of mathematics this should be an exciting topic for you. It can be somehow daunting for those who are not really mathematically inclined. Regardless, if you pay close attention you can get a grip of how it all works. When dealing with a number system we are talking about how numbers are handled in computers. Why are numbers that much of a big deal in computers? It is because computers can only understand digital language i.e. ones (1) and zeros (0). There are quite a number of number systems that are used in computers. In this article we shall be discussing the different types of number systems in computers. We will also look at some practical mathematical examples to buttress what we will be discussing.
Table of Contents
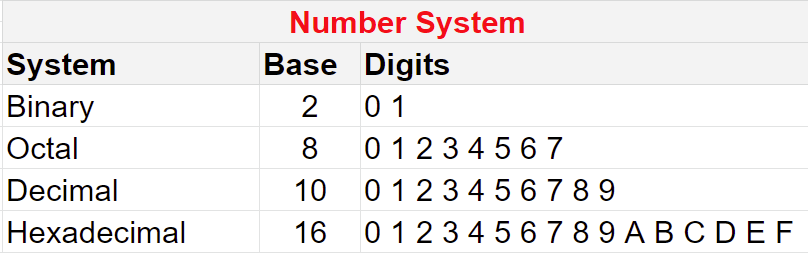
Decimal Number System
This is a common number system in computer which should be very easy for any of you to understand. Do you recall in your high school mathematics when we would deal with base ten (10) numbers? This is basically what we are dealing with here. Numbers that can be represented here can be comprised of any of the digits from zero (0) to nine (9). You must also obviously know that the value of a respective digit is a function of its position in a number.
For example, 5 in 205 is just 5 (or 5 x 100). Suppose the number is 502, 5 would be 500 hundred (or 5 x 102). It should be clear from that simple example how the position determines the value of a digit in a number. The takeaway from this is that the number to which you raise the power of 10 multiplying the respective digits in a number starts from 0 for the digit on the far right. As you move to the left, the power increases by 1 from digit to digit as you move along. For example, 50210 is (5 x 102) + (0 x 101) + (2 x 100).
Binary Number System
This is an important number system in computer. For this number system it means you are only representing numbers using just 1s and 0s. The decimal number system is essentially base ten. In case you have not noticed you should have seen a pattern. This means that the binary number system is base two (2). The aspect of digit position in a number comes into play just like it is for the decimal number system. The only difference is that you will be multiplying the respective digits with 2s raised to consecutive increasing powers.
This process of multiplying and adding the products will give a base ten (10) result. Before we look at an example it important to know that for this number system, the farthest right digit and the farthest left digit have particular names. They are least significant bit and most significant bit respectively. Let us consider 101010 as an example of a binary number. 1010102 is (1 x 25)+(0 x 24)+(1 x 23)+(0 x 22)+(1 x 21)+(0 x 20). That is (1 x 32)+(0 x 16)+(1 x 8)+(0 x 4)+(1 x 2)+(0 x 0) which is equals to 4210
We can also look at how the converse is done i.e. converting base 10 to base 2. Using the same number above it would be as follows:
| Divide 2 Into: | Write Remainder Here | |
| 2 | 42 | 0 |
| 2 | 21 | 1 |
| 2 | 10 | 0 |
| 2 | 5 | 1 |
| 2 | 2 | 0 |
| 2 | 1 | 1 |
| 0 | ||
| (↑read from bottom to top ) | ||
| Answer is 1010102 | ||
Octal Number System
The octal number system in computer also works on the same principles with the difference being that we are dealing with powers of 8. Digits used in representing numbers under this system lie from zero (0) to seven (7). The aspect of position of the digit is also taken into consideration. Let us suppose we have 7358 – let us calculate what that will be in base ten (10). 7358 is (7 x 82) + (3 x 81) + (5 x 80) thus 448 + 24 + 5 equals 47710
Using the above example, conversion from base 10 to base 8 will be as follows:
| Divide 8 Into: | Write Remainder Here | |
| 8 | 477 | 5 |
| 8 | 59 | 3 |
| 8 | 7 | 7 |
| 8 | 0 | |
| (↑read from bottom to top ) | ||
| Answer is 7358 | ||
Hexadecimal Number System
This number system is basically base sixteen (16). The hexadecimal number system is unique in that it has digits zero (0) to nine (9) plus A to F. A is 10, B is 11, C is 12, D is 13, E is 14 and F is 15. The aspect of digit position also comes into play and what is being raised to certain powers in 16. You must bear in mind that when there are letters, you replace them with their actual values when calculating. Let us look at an example: 32CB16 – (3 x 163)+(2 x 162)+(12 x 161)+(11 x 160) thus 12288 + 512 + 192 + 11 which is equals 1300310. The hexadecimal number system is mainly used in microprocessors and microcontrollers. This is an important number system in computers.
We can you use the example above to illustrate how to convert from base 10 to base 16. Here is how to do it:
| Divide 16 Into: | Write Remainder Here | |
| 16 | 13003 | 11 |
| 16 | 812 | 12 |
| 16 | 50 | 2 |
| 16 | 3 | 3 |
| 16 | 0 | |
| 16 | ||
| (↑read from bottom to top ) | ||
| Answer is 32CB16 | ||
We hope you will find this article useful in giving an understanding of the dynamics involved in number systems in computers. These conversions that we have been showing you give you a picture of the background conversions that occur inside a computer as it interfaces with input and output devices.